【改造赛博火星】第一期：历法——改造火星的时间密码

在火星改造计划中，历法不仅是时间的坐标，更是地质变化与文明演进的基准。本文简要介绍现有火星历法，并提出适用于长期研究的“赛博火星节气历”。

现有历法

火星的一天称为“sol”，比地球日长39分35秒。火星年约为687地球日（668.59 sol），接近地球两年。火星自转轴倾角25度，类似地球，因此存在四季，但因轨道偏心率大，季节长度差异显著：北半球春季194 sol，秋季仅142 sol。主流历法如下：

NASA实用计时法：探测器的“打卡日历”

最常用的“极简”历法，无月份，仅以sol编号^[1]。如“毅力号”着陆日为sol 0，次日为sol 1。配套“协调火星时”（MTC）以“子午线港”为基准，类似地球格林威治时间。

大流士火星历：殖民预备役历法

分24个月，每组6个月，前5个月28 sol，第6个月27 sol，年末加闰日。奇数年、能被10整除（非100倍数）、能被1000整除为闰年（669 sol），其余为平年（668 sol）^[2]。详见维基百科。

节气改编版：火星的“中国风”

有版本将24个月直接用二十四节气命名。

独创历法（火星节气历）

为什么要独创历法

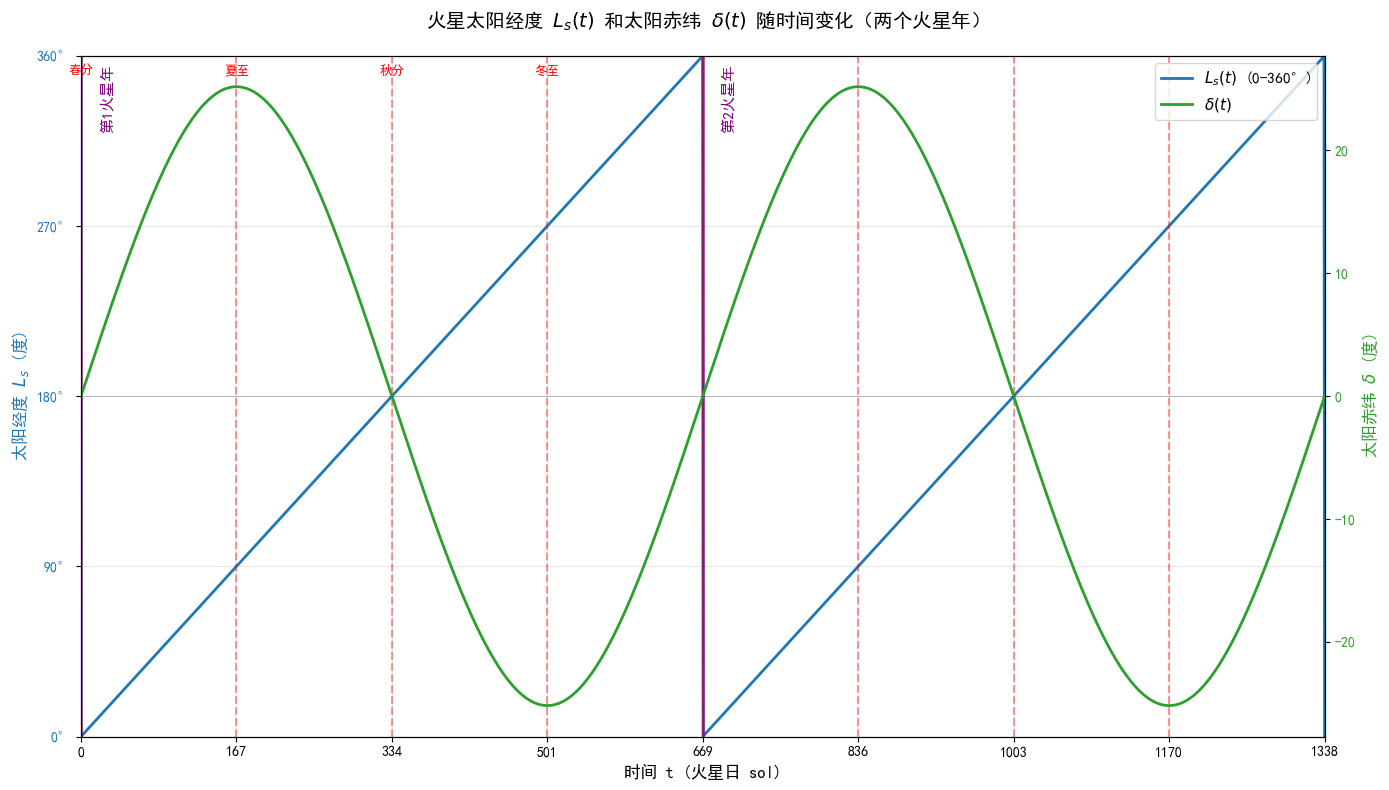
为研究火星长期地质与气候演化，需考虑岁差、章动等长周期天体力学现象。为此，本文构建火星太阳直射点纬度（火星版太阳赤纬函数^[3]）随时间变化的函数，据此确定节气点，并以节气为月首。

火星太阳赤纬函数

1. 匀速模型

在忽略其他天体影响、假设火星轨道为正圆时，可推导得太阳直射点纬度$\delta$关于时间$t$的函数：

$$\delta (t)=arcsin(sinL(t)\cdot sin\epsilon )$$

$L(t)$表示太阳在火星黄道上的平角位置，即太阳黄经函数：

$$L(t)=\omega \cdot t=\frac{2\pi t}{T}$$

自变量：

• $t$：时间，单位为火星秒

因变量:

• $\delta (t)$：太阳赤纬角，单位为度

常量：

• $\epsilon ={25.19}^{\circ }$：火星轴倾角
• $\omega =\frac{2\pi }{T}$：火星公转的平均角速度，其中公转周期$T=86400\cdot 686.6=59,322,240$火星秒

$L(t),\delta (t)$函数图像：

2. 椭圆模型

实际火星轨道偏心率较大($e\approx 0.0934$)，太阳在黄道上的角速度非匀速。需用开普勒方程求解太阳真实位置：

$$M=E-esinE$$

开普勒方程为超越方程，无解析解，常用数值法（如牛顿迭代法）求真近点角$\nu$。级数展开在$e\ll 1$时可用，但长期研究需牛顿法。$\nu (t)$可转化为$L(t)$：

$$L(t)=\nu (t)+\omega$$

• $\omega$：近心点黄经。

假设火星春分点（黄经0°）与近日点重合（实际会进动），对比椭圆与匀速模型太阳赤纬函数如下：

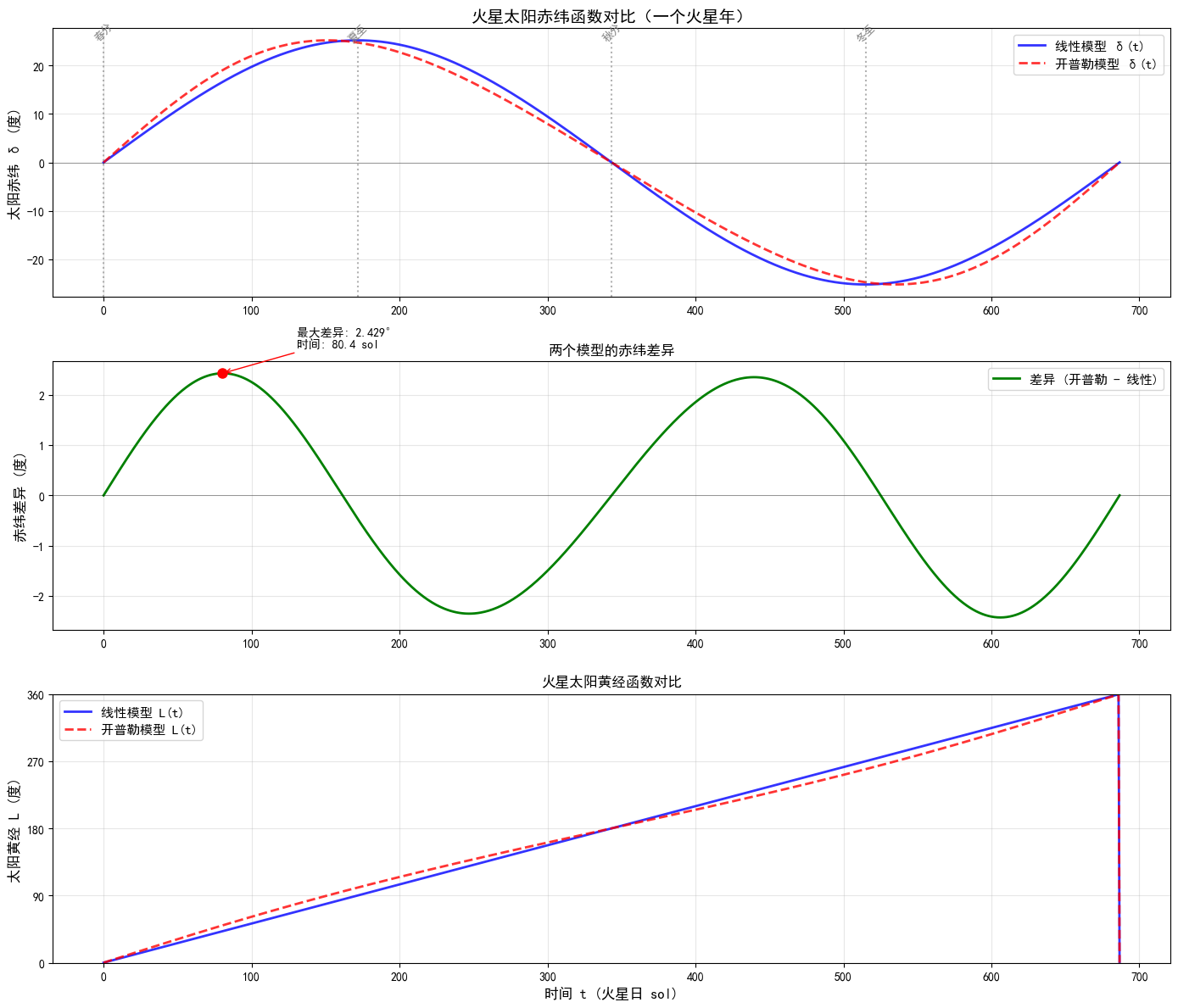
二者差异不大因设定近日点黄经为0。若考虑春分点进动（$\omega$随时间增加，进动周期约17万~92万年，本文取17万年为例），则$t=52747$年时季节已完全偏移：

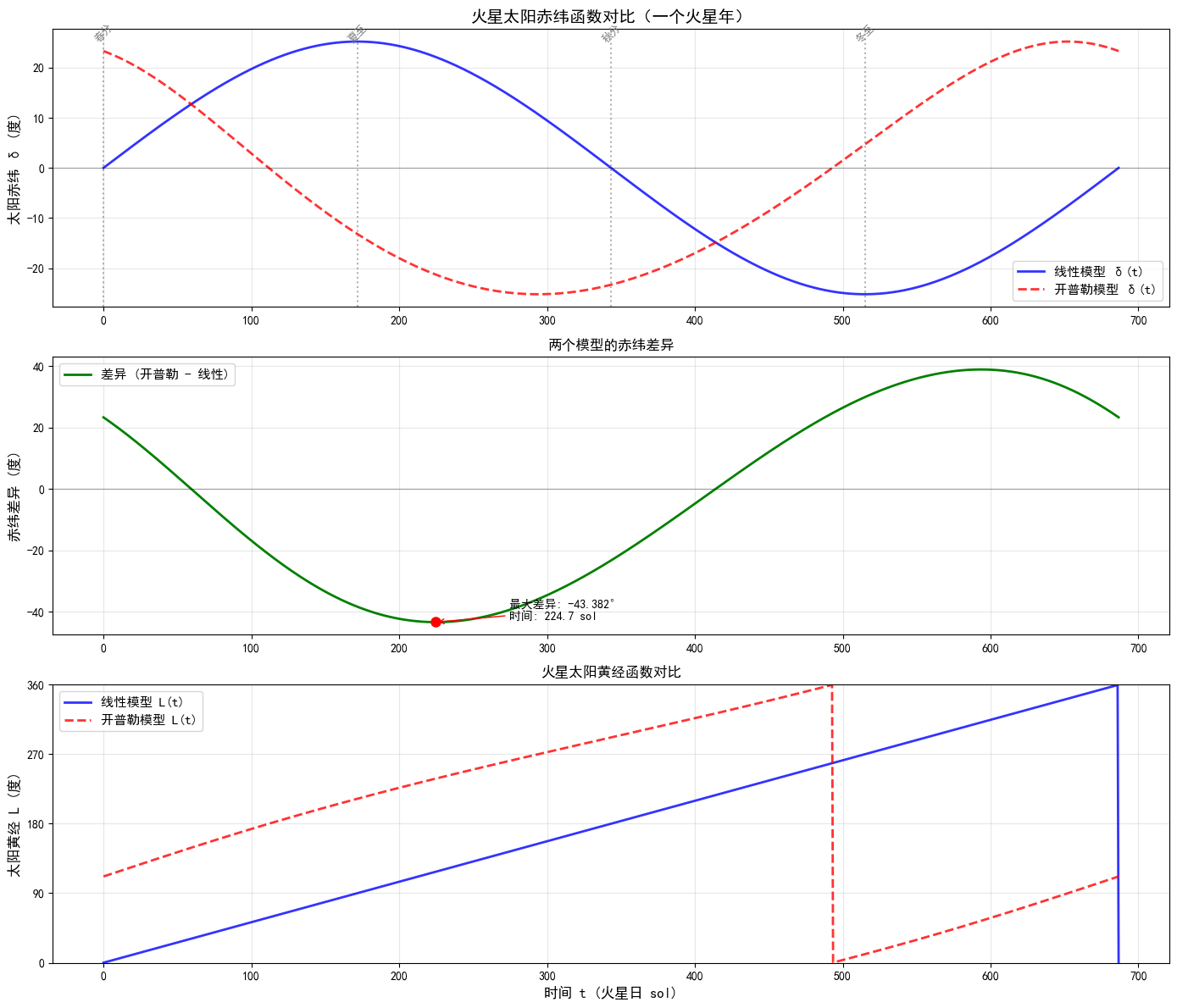
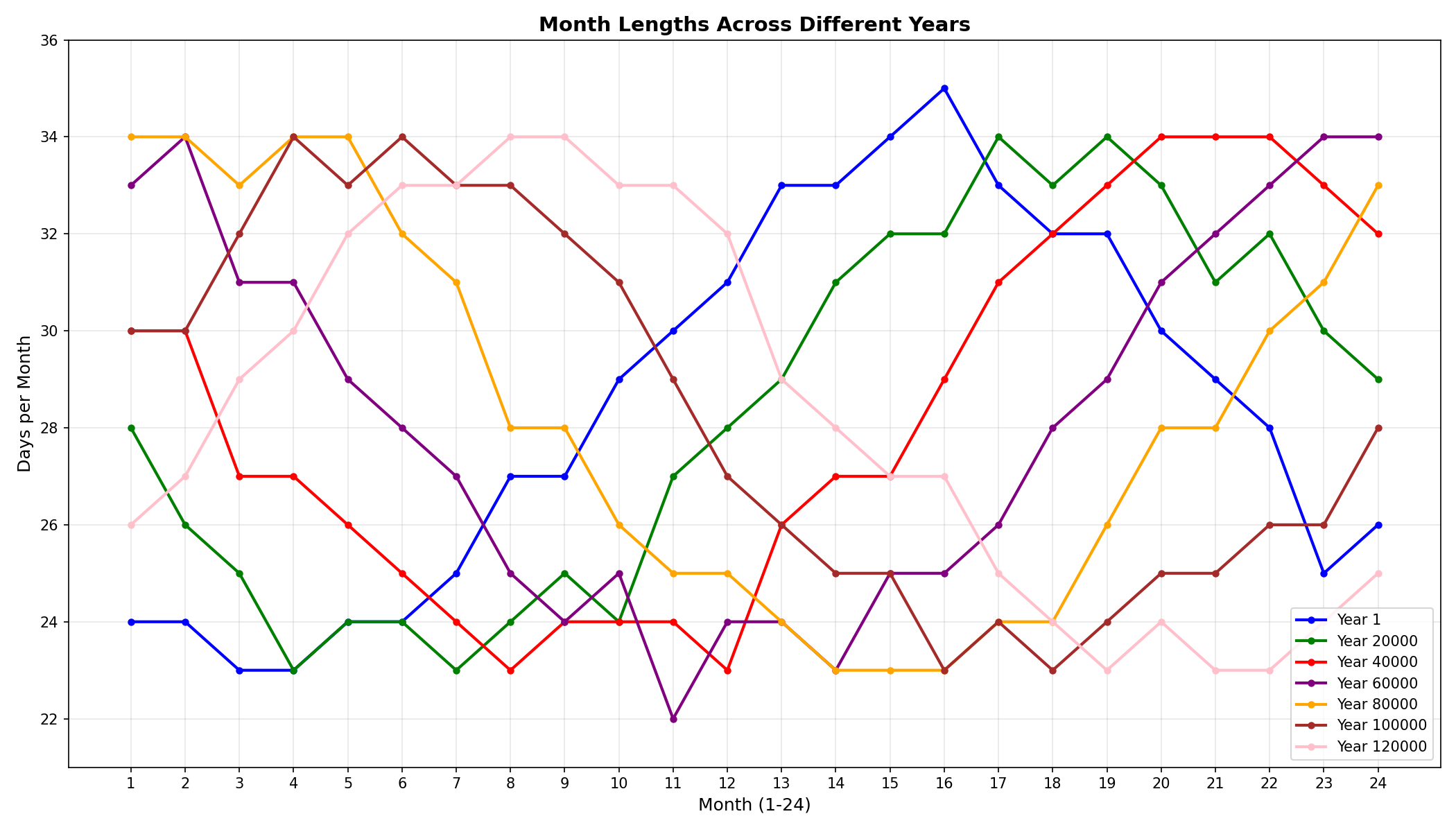
据此可数值解出考虑进动的太阳赤纬函数，进而计算任意年份节气点，形成适用于长期研究的节气历。下图为模型计算的12万年内各月天数，远日点月份明显后移。

3. 更进一步

春分点进动主要由岁差（自转轴绕黄道面法线运动）引起，同时导致黄赤交角变化。火星黄赤交角波动范围15-35°，周期约12.4万年^[4]。此变化不影响历法本身，但会引发气候周期变化。黄赤交角可视为时间函数$\epsilon (t)$，影响太阳赤纬函数：

$$\delta (t)=arcsin(sinL(t)\cdot sin\epsilon (t))$$

本文简化$\epsilon (t)$为周期函数（$\epsilon (t)={\epsilon }_0+\mathrm{\Delta }\epsilon \cdot sin(\frac{2\pi t}{T_2})$）以便分析。

总结

综上所述，火星节气历以节气为月首，动态调整月份长度，更真实地反映火星的季节与气候变化，为赛博火星的科学研究和未来活动提供统一、科学的时间基准，并为长期演化研究奠定基础。

附录

太阳赤纬函数推导

恒星的位置可以在不同的天球坐标系中表示：

• 黄道坐标系：以黄道为基准，坐标为黄经$L(t)$和黄纬$\beta =0$。
• 赤道坐标系：以行星赤道为基准，坐标为赤经$\alpha$和赤纬$\delta$。

我们先将黄道坐标转化为赤道坐标：

• $x=cos\beta \cdot cosL(t)$
• $y=cos\beta \cdot sinL(t)$
• $z=sin\beta$

因为$\beta =0$，所以：

• $x=cosL(t)$
• $y=sinL(t)$
• $z=0$

接下来进行绕$x$轴旋转（因为黄赤交角是两个平面之间的倾角），旋转角度为$\epsilon$，得到赤道坐标系中的坐标：

• $x^{\prime }=x=cosL(t)$
• $y^{\prime }=ycos\epsilon -zsin\epsilon =sinL(t)\cdot cos\epsilon$
• $z^{\prime }=ysin\epsilon +zcos\epsilon =sinL(t)\cdot sin\epsilon$

赤纬是赤道坐标系中向上的角度，即：

$$\delta (t)=arcsin(z^{\prime })=arcsin(sinL(t)\cdot sin\epsilon )$$

开普勒方程

$$M=E-esinE$$

其中：

• $M$是平均近点角（Mean Anomaly），与时间$t$成线性关系：$M=n(t-t_0)$，$n$是平均运动（Mean Motion），$t_0$是近地点通过时刻。
• $E$是偏近点角（Eccentric Anomaly）
• $e$是轨道离心率

$M$,$E$,$\nu$示意图：

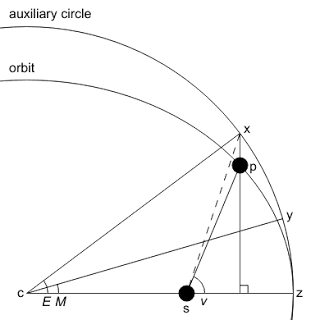
真近点角$\nu$与偏近点角$E$的关系为：

$$\tan \left(\frac{\nu }{2}\right)=\sqrt{\frac{1+e}{1-e}}\tan \left(\frac{E}{2}\right)$$

---

参考文献

---

1. NASA. Mars 2020 Mission Overview[EB/OL]. [2021]. [2025-10-21]. https://mars.nasa.gov/mars2020/mission/overview/. ↩︎

2. Darian calendar[EB/OL]. // Wikipedia. [2023-10-20]. [2025-10-21]. https://en.wikipedia.org/wiki/Darian_calendar. ↩︎

3. Declination[EB/OL]. // Wikipedia. [2025-10-22]. https://en.wikipedia.org/wiki/Declination. ↩︎

4. LASKAR J, CORREIA A C M, BOUE G, et al. Long term evolution and chaotic diffusion of the insolation quantities of Mars[J]. Icarus, 2004, 170(2): 343-364. ↩︎